Trigonometría es una palabra que deriva de dos términos griegos: por un lado, trigonos (τριγωνο trigōno) que significa triángulo y, por otro, metros (μετρον) que refiere a medida. Por lo tanto, el concepto que aquí empezamos a analizar hace alusión a la medida o medición de los triángulos.
Es una rama propia de las matemáticas cuya función principal es analizar y estudiar los elementos que componen un triángulo. Expresado de otro modo, interpreta cuestiones trigonométricas. Con esto nos referimos a:
- Seno-coseno
- Tangente- cotangente
- Secante-cosecante
Es importante destacar que esta área de las matemáticas estudia las relaciones que existen entre esos elementos y que se dan dentro de lo que se denomina el triángulo rectángulo. Es decir, un dibujo geométrico que cuenta con uno de sus lados a 90°.
Como rama de las matemáticas tiene una larga historia, puesto que se cree que existe hace más de tres mil años. Se adjudica el uso de la trigonometría a civilizaciones antiguas ya desaparecidas como, por ejemplo, los egipcios y los babilónicos. En ambas culturas se evidencia el empleo de los ángulos de los triángulos para la construcción de las inmensas pirámides que, en la actualidad, continúan en pie.

Asimismo, se afirma que la trigonometría fue aplicada en otras estructuras consideradas como complejas para la época en la cual fueron utilizadas.
Tanto es el estudio de esta área matemática que se ha llegado a realizar un mapa estelar usando como fundamento los conocimientos trigonométricos. En este sentido, la relación ha sido recíproca, es decir, tanto las estrellas como los astros han aportado al estudio de la trigonometría, como esta ha permitido calcular rutas, predecir fenómenos, establecer calendarios, etc.
Índice de temas
Funciones de la trigonometría.
La trigonometría cuenta con seis funciones básicas y fundamentales. Si bien las nombramos en la introducción de este artículo, vamos a intentar ampliarlas y detallarlas con más detenimiento.
Básicamente, al hablar de función trigonométrica hacemos alusión a un argumento o variable independiente que no es más que un ángulo. Entonces, las funciones lo que hacen es describir la medición de ángulos y de triángulos.
Antes de conocer estas mediciones es importante anticipar que, en las funciones trigonométricas, los ángulos también se expresan como radianes. Esta es otra de las formas que existen para medir un ángulo y su apertura. Además, permite conocer los grados que están en relación con el radio de una circunferencia.
Recordemos que, en trigonometría, el triángulo que se mide es aquel considerado como la base principal de esta rama matemática. Nos referimos al triángulo rectángulo.
Qué es el triángulo rectángulo.
El triángulo rectángulo es un tipo de polígono compuesto por tres lados. Uno de ellos es completamente recto, midiendo exactamente 90°. Por su parte, el lado del triángulo que, básicamente, delimita el ángulo recto, lleva por nombre cateto. Mientras que el lado opuesto y de mayor longitud se denomina hipotenusa.
Funciones o razones trigonométricas.
Como bien mencionamos, esta rama matemática cuenta con seis funciones que no son más que las relaciones que se dan entre los catetos y la hipotenusa de un triángulo rectángulo en relación, claro está, con uno de los ángulos agudos del mismo.
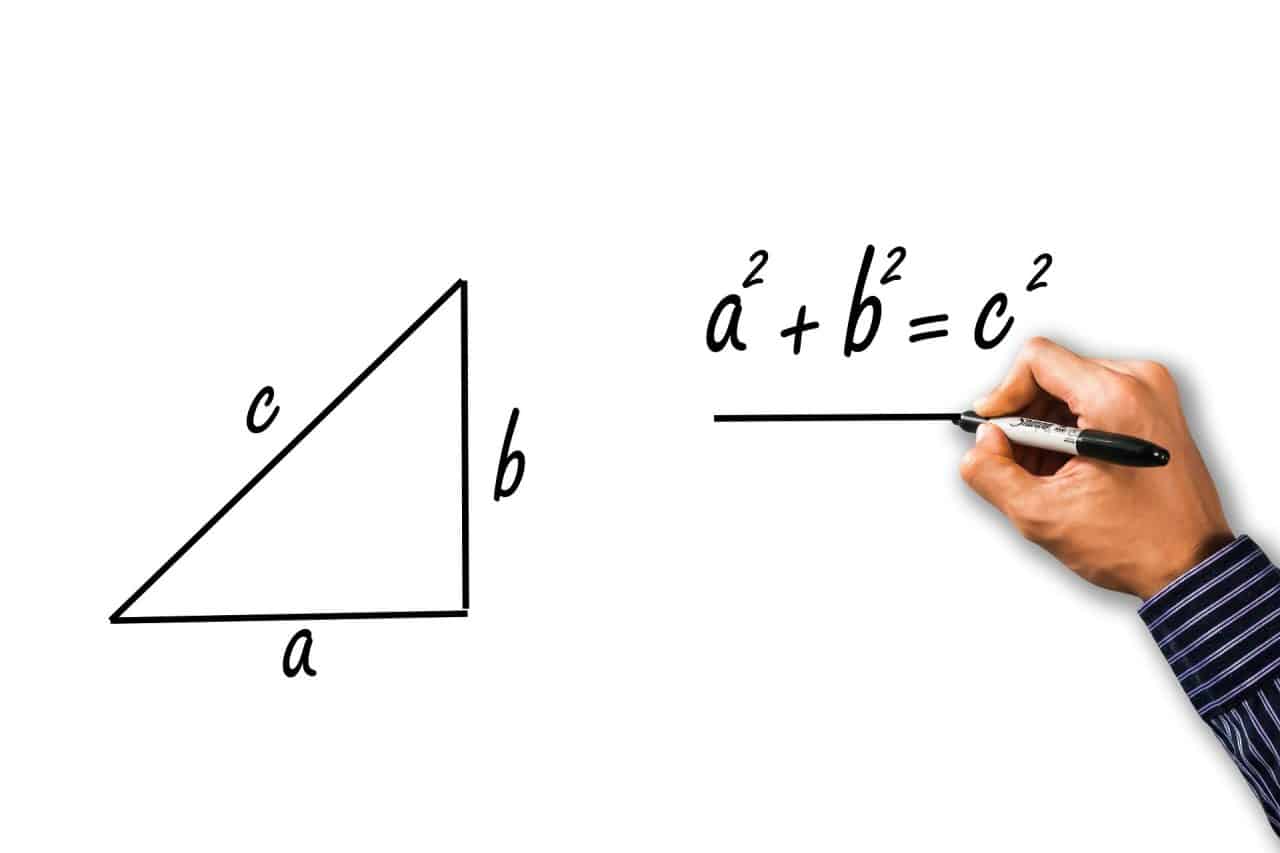
Entonces, para todo tipo de triángulo rectángulo existen seis tipos de funciones.
- Seno: se abrevia sen. Es la división entre la longitud del cateto opuesto y la longitud de la hipotenusa. El primero se conoce con el símbolo CO y el segundo, con el símbolo H.
- Coseno: se abrevia cos. Es la división entre la longitud del cateto adyacente y la longitud de la hipotenusa. La primera se simboliza CA y, la segunda, H.
- Tangente: se abrevia tan. Razón que se da entre la longitud del cateto opuesto (CO) entre el cateto adyacente (CA), que es igual a la división entre coseno y seno.
- Cotangente: se abrevia cot. Es la división que se da entre el cateto adyacente (CA) y el cateto opuesto (CO).
- Secante: se abrevia sec. Aquí se mide la razón entre la hipotenusa (H) y el cateto adyacente (CA).
- Cosecante: se abrevia csc. Razón entre el cateto opuesto (CO) y la hipotenusa (H).
Cuando se está analizando el gráfico de una función y en él se repiten las formas, se las clasifica como periódicas. Se las denomina, por lo tanto, funciones trigonométricas periódicas. Esto ocurre, por ejemplo, en un electrocardiograma.
Características de la trigonometría.
La trigonometría es una rama de la matemática que estudia las razones trigonométricas. Sin embargo, también puede estudiar las esferas dentro de lo que se conoce como geometría espacial. Sencillamente, porque que en cada cuadrante de una esfera, así como de un círculo, podemos encontrar triángulos rectángulos.
La trigonometría tiene la responsabilidad de calcular los elementos que conforman los triángulos a través del estudio de las relaciones que se da -o que existen- entre los ángulos y los lados de los mismos.
En este sentido, la trigonometría guarda una serie de características que la definen y anclan dentro del campo de las matemáticas.
- Utiliza unidades angulares para medir los ángulos: grado sexagesimal (divide una circunferencia en 360°), el radián (unidad que mide ángulos en una circunferencia completa, algo así como 2 π radianes) y el sistema decimal (se aplica en arquitectura, construcción y topografía).
- Identidad trigonométrica: igualdad que tiene como tarea vincular dos funciones trigonométricas. Estas funciones están unidas por operaciones racionales de exponentes enteros.
- Elementos principales de un ángulo: los lados, vértices (punto en el que se unen los lados) y su apertura o amplitud (medidos en grados o en radianes).

Para qué sirve la trigonometría.
La trigonometría ocupa un rol fundamental no solo dentro de las matemáticas sino también en la vida cotidiana. Cuando se requiere hacer cosas con precisión, siempre se aplica alguna rama de la matemática y, en este caso, la trigonometría es aplicable en varias situaciones.
Cuando hablamos de medir algo con precisión nos referimos a mediciones de distancia entre dos ubicaciones o puntos diferentes y distantes entre sí. Las técnicas trigonométricas permiten hacer diferentes operaciones que dan como resultado datos concretos y específicos. Los mismos que no dan lugar a error alguno.
En este sentido, la trigonometría es una rama matemática aplicada con frecuencia en los sistemas de navegación satelital. Asimismo, se utiliza con precisión en astronomía y para medir la distancia real entre diferentes puntos o zonas geográficas. De igual modo, se aprovecha en el campo de la física y las telecomunicaciones.
No por nada al origen de la trigonometría lo encontramos en la época antigua. En tiempos de egipcios y babilónicos se desarrollaron ciertos conocimientos que trabajaban sobre las proporciones de los triángulos. Esto les permitió crear edificaciones monumentales que se sostienen hasta el día de hoy. Sin embargo, por aquellos años no contaban con una medida de ángulo.
Estas grandes civilizaciones aplicaron la trigonometría a la vida diaria y la usaron, por ejemplo, para estudiar, conocer y anticipar la puesta del sol y de otros cuerpos celestes. Asimismo, aplicaron sus conocimientos en esta área matemática para analizar los movimientos planetarios y, para ello, se valieron de una tabla de secantes. La trigonometría más primitiva también permitió a los egipcios levantar las pirámides y demás obras de gran envergadura.
Citar este artículo
Navicelli, V. (26 de agosto de 2022). Definición de trigonometría. Funciones, características y para qué sirve. Definicion.com. https://definicion.com/trigonometria/



