La inconmensurabilidad es la propiedad de ser inconmensurable. Algo inconmensurable es aquello que no se puede mensurar, es decir, que no se puede medir, limitar o contabilizar por completo. La inconmensurabilidad es la propiedad de no poder ser medido ni abarcado por determinados límites de medición, ya que su naturaleza sobrepasa toda escala de medición conocida. De modo que, algo inconmensurable se refiere a aquello que es ilimitado, incontable, innumerable e incalculable.
El término está formado por el prefijo «in-» que indica negación o privación, más la palabra base «conmensurable», que significa medible, calculable, limitable, más el sufijo «-dad» que indica la sustantivación abstracta del adjetivo. El término «inconmensurabilidad» indica la propiedad de no ser medible, calculable o comparable con otra propiedad. Es el antónimo del término «conmensurabilidad» que indica la propiedad de poder ser medido, calculado y delimitado según determinados parámetros.
En sentido general, la palabra se usa para referirse a todo aquello que sobrepasa los límites de la medición, la comprensión o la posibilidad de abarcar algo por completo. De manera coloquial, suele usarse el término «inconmensurable» o «inconmensurabilidad» para hacer referencia a algo enorme, colosal, descomunal, gigantesco o excesivo. Por ejemplo «el tamaño del universo es inconmensurable» «la inconmensurable profundidad del océano» o «el amor de una madre es inconmensurable».
En matemática, la inconmensurabilidad es un concepto que expresa la falta de un medida común para la medición exacta y directa de dos o más variables diferenciadas. Por ejemplo, es inconmensurable la diagonal de un cuadrado respecto de su lado, pues sus longitudes no se pueden comparar entre sí. La inconmensurabilidad matemática no expresa la imposibilidad de comparación sino la falta de una medida común, es decir, la ausencia de una escala de medición que sirva para ambas variables.
En la ciencia y la filosofía, se llama inconmensurabilidad a la imposibilidad de medir o comparar directamente dos conceptos, magnitudes o teorías que son diferentes en su naturaleza o escala de medición. En términos científicos y filosóficos, la inconmensurabilidad refiere a la incomparabilidad de una teoría con otra, ya que existe una diferencia radical, disparidad o desigualdad fundamental entre ambas teorías.
En la filosofía de la ciencia, el concepto de inconmensurabilidad fue introducido en 1964 por los pensadores Thomas Kuhn y Paul Feyerabend. Ambos autores tomaron el concepto de las matemáticas y lo trasladaron al campo del estudio crítico del pensamiento científico. En su obra «La estructura de las revoluciones científicas» (1962), Kuhn concibió a la inconmensurabilidad como la diferencia o incompatibilidad que se da entre un paradigma científico y otro. Por su parte, Feyerabend concibió a la inconmensurabilidad como un cambio semántico irreconciliable en los términos de dos teorías distintas.

Índice de temas
Breve historia del descubrimiento de la inconmensurabilidad
Inconmensurabilidad en la filosofía de la ciencia
Ejemplos de teorías inconmensurables entre sí
Breve historia del descubrimiento de la inconmensurabilidad.
Según las concepción matemática de los antiguos griegos, todo los fenómenos y magnitudes del mundo se podían medir y contabilizar utilizando números enteros. Así, los antiguos griegos diseñaron su geometría, su aritmética e incluso su música, un ejemplo de esta concepción es la creación de la escala musical, conocida hoy en día como la escala pitagórica.
Sin embargo, fueron los propios pitagóricos quienes demostraron que la diagonal de un cuadrado y su lado no establecían una relación que pudiera ser expresada mediante números enteros, esto quiere decir que eran inconmensurables. Sin proponérselo, los pitagóricos habían descubierto la inconmensurabilidad.
Este descubrimiento, atribuido a Pitágoras, significó una profunda crisis del conocimiento y la propia cosmovisión del mundo antiguo. Pues, en una primera instancia, los pitagóricos buscaban descifrar todos los misterios del universo empleando números enteros. Sin embargo, el descubrimiento de la inconmensurabilidad destruyó el sistema basado en números enteros e introdujo, por primera vez, el concepto de los números irracionales, lo que produjo, además, no sólo un cambio en la concepción matemática sino en la idea total del mundo como lo concebían los antiguos griegos.
A propósito de esto, en su obra «Vida pitagórica» (s. III) Jámblico señala:
«Dicen que los dioses se enfurecieron con quien difundió la doctrina de Pitágoras, muriendo como un infame en el mar, por sacrílego al haber expuesto la doctrina de la inconmensurabilidad y los números irracionales».
La aparición de las magnitudes inconmensurables marcó un cambio radical en la historia de la geometría antigua, debido a que tiró por la borda el proyecto pitagórico de establecer al número como esencia fundamental del universo. El descubrimiento de la inconmensurabilidad desterró de la geometría la posibilidad de medir siempre con total exactitud e imprimió en la matemática antigua la tendencia geométrica-deductiva plasmada luego en «Los Elementos» de Euclides.
Los inconmensurables llevaron a una transformación lógica que estremeció los propios cimientos de la geometría antigua, ya que invalidó todas las pruebas matemáticas basadas en los teoremas de proporción pitagórica. De esta manera, el concepto de inconmensurabilidad provocó la primera crisis de las bases teóricas en la historia de la matemática.

Inconmensurabilidad en la filosofía de la ciencia.
En la filosofía de la ciencia, el concepto de inconmensurabilidad fue introducido por Thomas Kuhn y Paul Feyerabend, quienes tomaron el concepto de las matemáticas para aplicarlo al estudio crítico de las teorías científicas. Ambos autores introducen el concepto como parte fundamental de su crítica a la tesis del positivismo lógico sobre la acumulación del conocimiento científico, según la cual, el corpus del conocimiento científico presenta una continuidad y coherencia entre las teorías sucesivas. Según la concepción heredada del positivismo lógico o empírico, el conocimiento científico ha ido aumentando con el paso del tiempo de manera uniforme y homogénea. Tanto Kuhn como Feyerabend rechazan esta idea de la acumulación del conocimiento científico y, en su lugar, hablan de una discontinuidad y heterogeneidad irreductible entre las diversas teorías científicas.
Ambos autores presentan un concepto de ciencia radicalmente distinto al de la concepción heredada del positivismo. Las críticas tanto de Feyerabend como de Kuhn a la concepción clásica de la ciencia introducen conceptos como el de distinción, divergencia, discrepancia e irreductibilidad en la relación entre las diversas teorías científicas. En este marco, el concepto de inconmensurabilidad es de vital importancia, ya que hace referencia al problema de la no correspondencia e incompatibilidad entre las teorías científicas.
Otra tesis que busca respaldar la acumulación y coherencia del conocimiento científico postula la existencia de un lenguaje neutro que sirva de contraste para que puedan probarse y mediarse dos teorías en competencia. De esta manera, el leguaje neutro permitiría exponer las consecuencias empíricas de ambas teorías, a partir de lo cual se podría determinar cuál de ambas es la que presenta el mayor contenido empírico verificado. Esta tesis implica, a su vez, otras dos hipótesis referentes a la coherencia del conocimiento científico:
- Ambas teorías deben presentar la propiedad de la intertraductibilidad, es decir, que una teoría sea traducible a los términos de la otra y viceversa: entre una teoría T y la teoría sucesora T1 deben poder traducirse sin problemas sus términos teóricos.
- En el caso de la teoría del falsacionismo de Karl Popper, además, ambas teorías deben presentar deductibilidad, donde T1 debe deducirse lógicamente de T.
Sin embargo, la inconmensurabilidad hace imposible la viabilidad de las tesis clásicas de la coherencia científica, tanto de la traductibilidad como la deductibilidad. Pues, en el primer caso, la inconmensurabilidad muestra que ciertos resultados empíricos entre dos teorías sucesivas tienden a perderse. En el segundo caso, queda invalidada la tesis ya que al afirmar que puede existir deductibilidad entre dos teorías sin la existencia de un lenguaje neutro que las ponga en contraste invalida la propia tesis.

La inconmensurabilidad de Thomas Kuhn.
En su obra «La estructura de las revoluciones científicas» (1962), Thomas Kuhn desarrolla un estudio clave para la sociología del conocimiento y la epistemología. En esta obra, Kuhn presenta el problema de la continuidad histórica del conocimiento científico, planteando la idea que las revoluciones científicas establecen cambios de paradigma en la estructura del conocimiento científico a través de la historia.
Kuhn cuestionó la idea de que exista una continuidad totalmente coherente y lineal en el desarrollo histórico del conocimiento científico. Al estudiar la Física de Aristóteles y la física de Newton, concluyó que sus conceptos no representaban una continuidad creciente, donde la teoría del Newton superaba e incluía la teoría de Aristóteles, sino que simplemente ambos modelos de conocimiento eran distintos. Para explicar esta discontinuidad y diferencia histórica de las teorías científicas estableció los conceptos de paradigma y cambio de paradigma para postular la idea de que la ciencia no presenta un progreso lineal y creciente sino que cambia a través de diversos paradigmas de conocimiento a los que llamó «revoluciones científicas».
En este marco, Kuhn introduce el concepto de inconmensurabilidad y lo describe como una propiedad global que expresa la relación entre paradigmas científicos sucesivos. En este sentido, un paradigma científico es inconmensurable desde las categorías de otro paradigma científico, por lo que la continuidad queda interrumpida por una disimilitud debido a la singularidad y unicidad de cada paradigma.

El concepto de inconmensurabilidad de Kuhn va más allá del campo semántico y se extiende a todo el conjunto de prácticas, técnicas y conceptos propios de la ciencia en cada momento histórico. Según Kuhn, afirmar que dos teorías son inconmensurables entre sí implica afirmar que no existe un lenguaje común para vincularlas, es decir, que no hay un lenguaje neutral a partir del cual ambas teorías podrían traducirse sin necesidad de resto o pérdida. De esta manera, los términos que mantienen sus significados a raíz de un cambio de paradigma o revolución científica hacen de base para el debate de las diferencias entre un paradigma y el otro y sirven a las comparaciones relevantes en la elección de teorías. En este sentido, la contrastación es, para Kuhn, un proceso que permite comparar dos teorías unidas por un conjunto de términos comunes, pero no sirve como método para evaluar teorías por separado.
La tesis de la inconmensurabilidad de Kuhn pone en cuestión y problematiza seriamente el concepto de una acumulación del conocimiento científico y la idea misma de un lenguaje neutral para la contrastación de teorías distintas, sin por eso caer en el irracionalismo ni en la irrelevancia del ámbito común de las teorías científicas.
La inconmensurabilidad de Paul Feyerabend.
El concepto de inconmensurabilidad de Paul Feyerabend se ubica en el ámbito semántico, donde el cambio sustancial en los términos centrales de una teoría invade completamente los términos de la nueva teoría, provocando que entre T y T1 no exista ningún resultado empírico en común. Feyerabend presenta esta noción de inconmensurabilidad semántica en el marco de su crítica a la tesis de acumulación del conocimiento científico y al panracionalismo en la ciencia.
En su obra «Contra el método» (1975) cuyo subtítulo es «Esquema de una teoría anarquista del conocimiento», Feyerabend despliega una aguda crítica a los conceptos clásicos de la ciencia, introduciendo la idea del irracionalismo en el pensamiento científico y una concepción anárquica del desarrollo de la ciencia. En este marco, Feyerabend introduce el concepto de inconmensurabilidad en contraposición con el racionalismo crítico de Karl Popper.
Feyerabend señala que, según el modelo de Popper, la investigación científica empieza con un problema. El problema surge a partir del conflicto entre una expectativa y una observación, la cual, a su vez, es elaborada por la propia expectativa. Feyerabend concluye, entonces, que la metodología de la ciencia consiste en resolver problemas inventando nuevas teorías que sean relevantes para el caso y falsables en términos popperianos. Una vez que la nueva teoría o teoría alternativa esté planteada, se da lugar a la fase crítica respecto de la relación entre una teoría (T) y la otra (T1), la cual debe responder a dos preguntas fundamentales:
- ¿Por qué la primera teoría (T) había tenido éxito hasta el momento?
- ¿Por qué ahora la teoría ha fracasado?
Si es posible que la nueva teoría (T1) responda satisfactoriamente a ambas preguntas, entonces, la teoría anterior (T) es descartada y superada por la nueva teoría. De manera que, para que una teoría nueva (T1) sea sucesora de la teoría anterior (T) debe presentar tres tipos de características:
- Clase A: Predecir un conjunto de eventos empíricos adicionales que la teoría anterior no predecía.
- Clase S: Presentar un conjunto de predicciones exitosas que coincidan, en cierto modo, con la teoría refutada, las cuales constituirán el contenido de verdad de la nueva teoría (T1).
- Clase F: Excluir los contenidos falsos de la teoría anterior, los cuales constituirán el contenido de falsedad de la nueva teoría (T1).
No obstante, Feyerabend aclara que la inconmensurabilidad entre T y T1 depende de la interpretación semántica que se les dé a las teorías. Si la teoría es de carácter instrumental, toda teoría remite a un mismo lenguaje de observación, en este caso las teorías son conmensurables. Sin embargo, Feyerabend señala que, incluso en los casos de interpretación instrumentalista, existen ciertos enunciados teóricos cuyo valor de verdad no depende exclusivamente de los enunciados observacionales (empíricos) sino que están sometidos a los criterios de evaluación anclados en las propias teorías. De esta manera, Feyerabend concluye que la posición instrumentalista sólo se concentra en los enunciados empíricos dejando de lado los criterios para relacionar los conceptos entre ambas teorías.
Ejemplos de teorías inconmensurables entre sí.
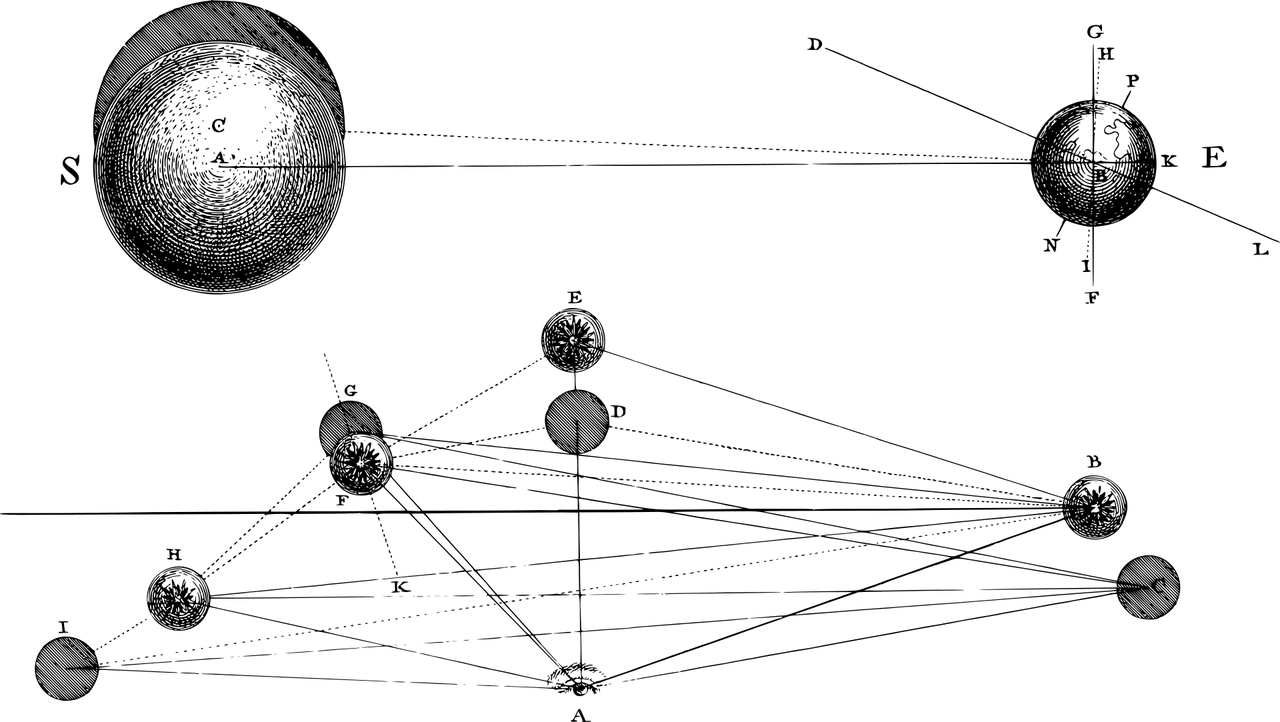
Cosmología ptolemaica vs cosmología copernicana.
La relación entre estas teorías es un ejemplo de inconmensurabilidad, ya que una ofrece un modelo geocéntrico del universo (ptolemaica) y la otra, un modelo heliocéntrico del universo (copernicana). La visión geocéntrica presentada por Ptolomeo plantea a la Tierra como centro del universo, la cual se mantiene fija mientras los otros planetas orbitan a su alrededor. Los postulados centrales de esta teoría se pueden resumir en 3:
- La Tierra es estática y a su alrededor orbitan los planetas.
- La Tierra es el centro del universo.
- El universo es finito y termina en un muro de estrellas fijas.
Por otro lado, la visión heliocéntrica planteada por Copérnico se diferencia radicalmente en sus postulados básicos de la teoría geocéntrica. En primer lugar, la cosmología copernicana establece al Sol como centro estático del universo, de manera que, la Tierra y el resto de los planetas giran entorno al Sol. La teoría copernicana cambia el eje central del universo y otorga movimiento a la Tierra. De esta manera, ambas teorías presentan una importante contradicción esencial en sus postulados, por lo que pueden considerarse teorías inconmensurables entre sí, ya que los términos de una teoría no son transferibles o traducibles a los términos de la otra.
Física clásica vs física relativista.
Se llama física clásica a la física basada en el modelo de la mecánica newtoniana y física relativista al modelo basado en la Teoría de la relatividad de Albert Einstein. Ambos modelos teóricos presentan tanto similitudes como radicales diferencias, pero, en sentido general, se consideran teorías incompatibles, es decir, inconmensurables.
Una de las principales diferencias entre ambos modelos físicos de explicar el mundo son los conceptos de espacio y tiempo. Mientras en la física clásica, basada en las leyes de Newton, tanto el tiempo como el espacio son considerados magnitudes absolutas y uniformes, para la física relativista de Albert Einstein, el tiempo y el espacio son magnitudes relativas a la posición específica de un observador. Mientras que para la física newtoniana, tanto tiempo y espacio no son variables sino magnitudes absolutas, en la física relativista de Einstein, ambas magnitudes son flexibles y dependen de la posición, velocidad y masa de un observador determinado.
De esta manera, la física relativista modifica sustancialmente los postulados de la física clásica. Tanto el tiempo como el espacio absolutos de la física clásica quedaron refutados cuando se demostró que no existía ningún tipo de referencia espacial que sea inmóvil ni tampoco la existencia de un tiempo universal. Para representar el concepto de tiempo relativo, Einstein presentó la paradoja de los gemelos, en la que explica que si un hombre viajara al espacio a una velocidad cercana a la velocidad de la luz dejando en la Tierra a su hermano gemelo, al volver, en la Tierra habrían pasado unos 50 años, mientras que para el viajero sólo pasarían 20. De esta manera, se produce un desfasaje en el paso del tiempo, debido a que el tiempo se ajustó a la la velocidad de movimiento de relativa a cada observador.
Por otro lado, también se modificaron los conceptos de masa y energía. Einstein elaboró su famosa fórmula «E = m.c2», donde «E» es energía; «m» masa y «c», la velocidad de la luz, para explicar que la masa y la energía son valores equivalentes. De modo que, en la teoría relativista, masa y energía representan expresiones distintas de una misma cosa: lo que se conoce con el nombre de «masa-energía».
Otra magnitud que se modifica con la física relativista es la de la longitud. Einstein postuló que cualquier objeto que viajara a la velocidad de la luz se encogería hasta alcanzar la longitud cero. Este fenómeno se conoce con el nombre de longitud relativa, ya que la longitud de un cuerpo es relativa a la velocidad de movimiento del mismo cuerpo o del observador que mide su longitud. Por lo que cada objeto tenderá a agrandarse o o encogerse según la perspectiva relativa para cada observador.
Física cuántica vs física clásica.
La física relativista y la física cuántica se consideran los dos pilares fundamentales de la física teórica contemporánea. Sin embargo, el principal problema de la física teórica es que ambos modelos físicos son considerados incompatibles entre sí, es decir, inconmensurables. Por un lado, la física o mecánica clásica es efectiva para medir y estudiar los fenómenos de los sistemas a gran escala (macrocosmos), mientras que la física o mecánica cuántica es efectiva para medir y explicar los fenómenos de los sistemas de escala pequeña (microcosmos). Pero cuando se intenta combinar las metodologías de ambas teorías para construir una sola teoría integral que las unifique, sus términos resultan ser incompatibles entre sí. Si se aplicaran las fórmulas que dan resultado a nivel cuántico en el marco de la física clásica, sus ecuaciones llevarían a absurdos impensados y, viceversa, si intentáramos resolver los problemas cuánticos con las ecuaciones propias de la física clásica, el resultado sería el mismo absurdo.
Las principales diferencias entre la física clásica y la física cuántica son:
| FÍSICA CLÁSICA | FÍSICA CUÁNTICA |
| Explica fenómenos a gran escala | Explica fenómenos a escala subatómica |
| Estudia el movimiento de los cuerpos | Estudia el movimiento de las partículas |
| Velocidades inferiores a la velocidad de la luz | Velocidades cercanas a la velocidad de la luz |
| Su estructura es determinista | Su estructura es probabilística |
| Observa el fenómeno sin modificarlo | El fenómeno se modifica según el observador |
| No es aplicable a nivel subatómico | Es aplicable a cualquier escala |
Citar este artículo
Aci, E. M. (11 de septiembre de 2024). Definición de inconmensurabilidad. Significados, surgimiento histórico, importancia en la filosofía, la física y las ciencias. Definicion.com. https://definicion.com/inconmensurabilidad/



