Definición de corolario

Un corolario es una consecuencia lógica que se sigue necesariamente de una verdad demostrada. Se considera una conclusión obvia e inevitable que es consecuencia de una verdad previamente establecida. En pocas palabras, un corolario es una verdad evidente que no necesita de una demostración empírica para ser corroborada.

En lógica y matemática, se llama corolario a toda proposición que se deduce necesariamente de premisas verdaderas, en el caso de la lógica, y de teoremas establecidos en el caso de la matemática. Por ejemplo, la suma de los lados de cualquier triángulo siempre dará 180°, este resultado es el corolario de una propiedad matemática previamente demostrada.

En lógica, un corolario es el resultado de una deducción o inferencia basada en premisas verdaderas. La estructura lógica del silogismo permite extraer conclusiones válidas a partir de premisas verdaderas. Un ejemplo de corolario en lógica lo podemos ver en el siguiente silogismo:

• Premisa 1: «Todos los hombres son mortales».
• Premisa 2: «Sócrates es hombre».
• Conclusión o corolario: «Sócrates es mortal».

Que «Sócrates es mortal» es un corolario que se deduce necesariamente de las premisas anteriores. De manera que, un corolario es una secuela o implicación necesaria y evidente de un conjunto de verdades anteriormente demostradas.

En sentido amplio, se puede llamar corolario a cualquier consecuencia inevitable, obvia o evidente de algo. Por ejemplo, el corolario del tabaquismo es una enfermedad respiratoria; el corolario de no pagar las cuentas es la cancelación de los servicios; el corolario de cometer un crimen es ir a la cárcel.

La etimología del término corolario proviene del latín «corollarium» o «corolla» que se traduce literalmente como «corona de flores» o «coronilla». Los antiguos romanos utilizaron el término para múltiples funciones:

1. Como adorno que se entregaba en agradecimiento a los actores al final de una obra dramática.
2. En un debate oratorio, se entregaba un «corollarium» a aquellos oradores que lograban demostrar con pruebas lógicas un argumento, razonamiento o postulado. De esta última acepción deriva finalmente el término corolario en referencia a la culminación o conclusión lógica de un razonamiento.

Características de un corolario.

• Derivación: Un corolario siempre deriva de una verdad previamente establecida. Esto quiere decir que no es una verdad por sí misma sino que es una conclusión que se sigue de algún axioma o fundamento anteriormente establecido. El corolario siempre es una consecuencia de alguna base o supuesto anteriormente demostrado.
• Consecuencia lógica: En la estructura de un razonamiento, un corolario siempre es una consecuencia lógica de una proposición original, es decir, aquello que lógicamente se sigue de las premisas o axiomas previos. Sigue una relación de causalidad y de conectividad lógica entre las premisas y la conclusión.
• Evidencia: Un corolario se considera evidente por sí mismo en tanto que se fundamenta en la verdad de las premisas. Esto quiere decir que no requiere prueba o evidencia adicional para ser demostrado. La verdad de las premisas demuestra la verdad de su corolario.
• Necesidad: Un corolario es una consecuencia lógica que se sigue necesariamente de las afirmaciones anteriores. Esto significa que la consecuencia (corolario) es necesaria e inevitable según la verdad de las premisas. Por ejemplo: Si es de día, entonces es necesario que el sol esté en el cielo.

Corolario en matemática.

En matemática, un corolario es un término utilizado para designar la evidencia de un teorema previamente demostrado, sin necesidad de otra forma de demostración. En términos matemáticos, un corolario es aquella conclusión que se deduce matemáticamente de algún teorema ya demostrado y que, por ende, no necesita de otra demostración más que su consecuencia matemática. En lenguaje matemático, es importante la distinción entre teorema, lema y corolario:

• Teorema: Es una proposición que parte de una hipótesis cuya verdad se demuestra, es decir, que la hipótesis del teorema afirma una tesis que no es evidente por sí misma y debe ser demostrada. El teorema confirma la verdad de la hipótesis. Una vez establecido el teorema, es posible extraer de él lemas y corolarios.
• Corolario: Es una afirmación que se sigue lógicamente de un teorema. La verdad del corolario no debe ser demostrada debido a que ya fue demostrada la verdad del teorema del cual deriva. Una proposición A es corolario de un teorema B si A puede deducirse lógicamente de B.
• Lema: Es una afirmación o proposición simple que se deriva de un teorema.

Ejemplos de corolarios en matemática.

Teorema de Pitágoras.

El teorema de Pitágoras afirma que:

«El cuadrado de una hipotenusa es igual a la suma de los cuadrados de los catetos».

De esta afirmación se sigue el corolario:

«La longitud de un cateto es menor que la longitud de la hipotenusa».

Formulación matemática:

• Teorema: a2 + b2 = c2
• Corolario: De a2 = b2 + c2 resulta b2 = a2 – c2

Suma de los lados del triángulo.

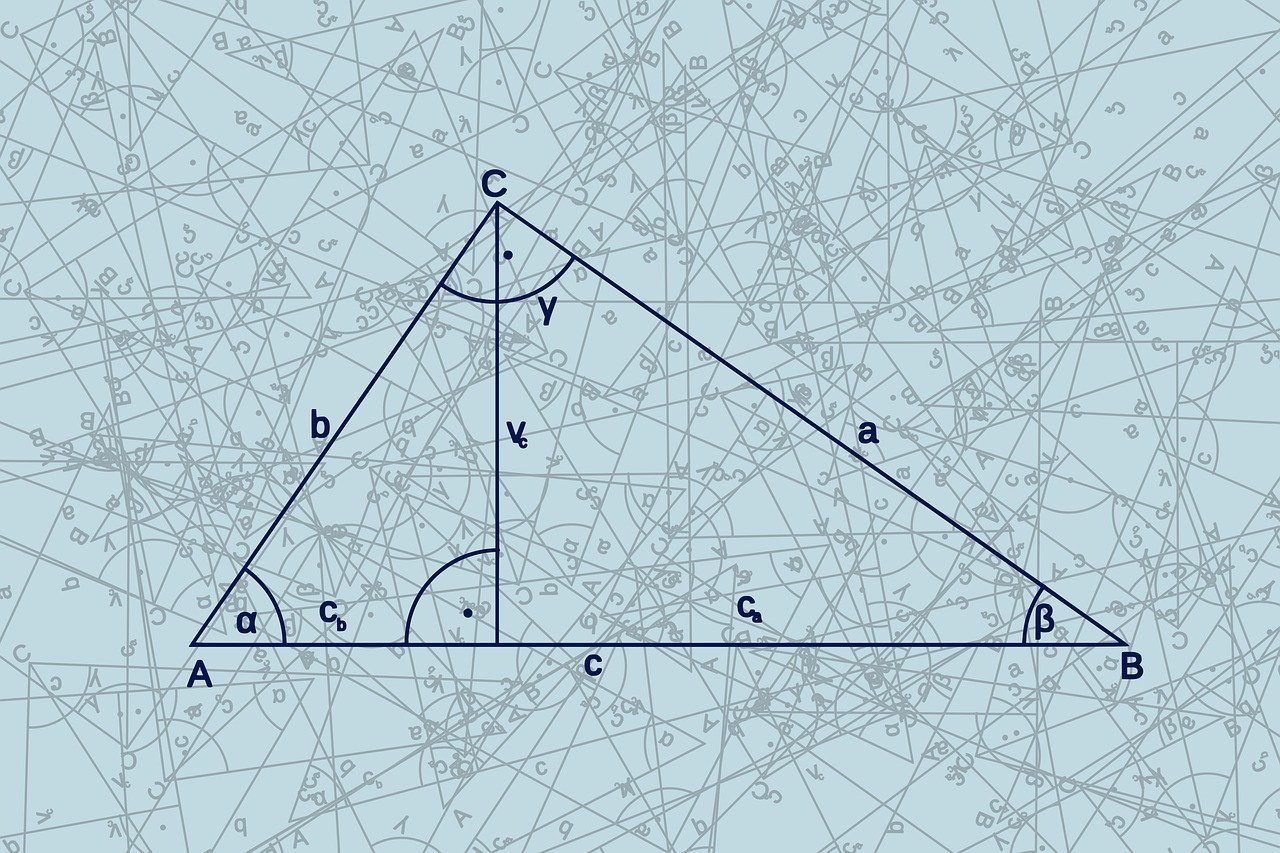
La suma de los lados de un triángulo siempre da 180°. De esta afirmación, se obtienen los siguientes corolarios:

• Corolario 1: La suma de los ángulos agudos de un triángulo rectángulo siempre da 90°.
• Corolario 2: Si dos ángulos de un triángulo son congruentes con otros dos ángulos de otro triángulo, entonces el tercer ángulo también es congruente entre ambos.
• Corolario 3: Un triángulo no puede presentar más de un ángulo recto ni más de un ángulo obtuso.

El corolario en la geometría euclidiana.

La geometría euclidiana es un sistema matemático desarrollado por el geómetra griego Euclides, en su obra «Elementos» (300 a. C). El sistema de Euclides consiste en establecer un conjunto de axiomas matemáticos intuitivamente aceptables como verdades autoevidentes, a partir de las cuales extraer otras proposiciones, teoremas y corolarios, cuya verdad es demostrada a partir de la verdad de los axiomas.

El sistema axiomático que inaugura Euclides tiene, en su estructura, al corolario como aquella proposición evidente que se deriva de la verdad de los axiomas o teoremas y que, por ende, no necesita de otra demostración particular más que su deducción lógica. En este sentido, Euclides es el primer matemático en introducir el sistema axiomático como método de estudio de la geometría y la matemática clásicas. A partir de los siguientes cinco axiomas y cinco postulados básicos, Euclides construye la base teórica de la geometría plana o parabólica:

Los 5 axiomas de la geometría euclidiana.

1. Propiedad transitiva: «Dos cosas iguales a una tercera, son iguales entre sí».
2. Suma de igualdad: «Si a cosas iguales añadimos otras cosas iguales, las sumas totales son iguales».
3. Igualdad de la resta: «Si a cosas iguales le restamos otras cosas iguales, los restos son iguales».
4. Propiedad reflexiva: «Las cosas que se superponen son iguales».
5. «El todo es mayor que la parte».

La presentación de la geometría de Euclides se realiza a partir de estos axiomas básicos tomados como verdades autoevidentes. El sistema axiomático de Euclides extrae todos los teoremas y corolarios de este conjunto de axiomas básicos de la geometría clásica.

Los 5 postulados de la geometría euclidiana.

1. «Dos puntos distintos determinan el segmento de una recta».
2. «Un segmento de recta puede extenderse infinitamente en una línea recta».
3. «Dados un centro y un radio cualquiera, puede establecerse una circunferencia».
4. «Todos los ángulos rectos son iguales entre sí».
5. «Por un punto exterior a una recta puede trazarse sólo una paralela».

A partir de estos cinco postulados, Euclides construye la teoría básica de la geometría plana y la geometría sólida de tres dimensiones. Se trata de una geometría sintética, ya que parte de axiomas que expresan las propiedades básicas de los objetos geométricos, como líneas y puntos, llevadas a un un conjunto de proposiciones sobre tales objetos.

Corolario en lógica.

En lógica y teoría de la argumentación, un corolario se define como una proposición que no necesita de una prueba particular, ya que se deduce necesariamente de las premisas o axiomas previos.

Un silogismo lógico es un razonamiento deductivo compuesto de tres proposiciones, donde la conclusión (corolario) se sigue lógicamente de las premisas. La estructura del silogismo permite formular conclusiones verdaderas a partir de la verdad de las premisas. En un silogismo, el corolario se identifica con la conclusión, la cual es verdadera, en tanto y en cuanto, sus premisas son verdaderas. Un silogismo se compone de:

1. Premisa mayor: Establece una regla general (generalización). Ej.: «Todos los hombres son mortales».
2. Premisa menor: Introduce un caso específico vinculado con la regla general (particularización o especificación). Ej.: «Sócrates es hombre».
3. Conclusión o corolario: Expresa la consecuencia lógica que se sigue necesariamente de las premisas. Ej.: «Sócrates es mortal».

Otros ejemplos de silogismos:

1. PM: «Todos los leones son felinos».
2. Pm: «Simba es un león».
3. C: «Simba es un felino».

1. PM: «Ningún ser humano puede volar».
2. Pm: «Juan es un ser humano».
3. C: «Juan no puede volar».

1. PM: «Todas las flores se marchitan».
2. Pm: «Las rosas son flores».
3. C: «Las rosas se marchitan».

En lógica, el corolario siempre es la conclusión, ya que es aquello que se deduce lógicamente de las premisas. El silogismo establece una relación de enlace y continuidad entre las premisas y la conclusión, lo cual permite una progresión y ampliación del contenido de las proposiciones.

Corolario en la filosofía.

En filosofía, el corolario ha sido utilizado por los filósofos como un conjunto de proposiciones que se derivan de determinado sistema filosófico basado en axiomas o supuestos previamente establecidos. Si bien, no se ha utilizado el término «corolario» por sí mismo, salvo en casos como el de Spinoza, el concepto de una consecuencia filosófica que se deriva de la verdad de un sistema axiomático ha sido ampliamente utilizada a lo largo de la historia de la filosofía.

Quien sí utiliza el término corolario propiamente dicho es Spinoza, en su obra «Ética demostrada según el orden geométrico», donde desarrolla un sistema filosófico que imita el sistema axiomático-geométrico de Euclides. El sistema filosófico de Spinoza parte de una demostración geométrica de la ética y la metafísica, a partir de definiciones y axiomas, de los cuales se deriva un conjunto de lemas y corolarios.

La «Ética» de Spinoza está escrita siguiendo la estructura del pensamiento geométrico-matemático, un sistema basado en ciertos axiomas a partir de los cuales se extraen corolarios como conclusiones válidas. Spinoza intentó aplicar el sistema de Euclides, propio de la geometría, para desarrollar una demostración filosófica basada en un esquema deductivo, mediante definiciones y axiomas.

La estructura de la obra de Spinoza es la siguiente:

• Definiciones: Establece la definición de los conceptos centrales de su sistema filosófico, tales como «sustancia», «Dios», «cuerpo», «alma», etc.
• Axiomas: A partir de las definiciones, establece los axiomas más importantes como verdades autoevidentes.
• Proposiciones: Son afirmaciones asociadas al sistema axiomático y las definiciones, que no se demuestran por sí mismas pero que permiten el desarrollo de las ideas en el marco del sistema.
• Lemas: Se trata de proposiciones menores deducidas de los axiomas y definiciones.
• Corolarios: Extrae conclusiones válidas a partir de la verdad del sistema axiomático previamente establecido.
• Escolios: Se trata de notas complementarias para la explicación de los axiomas y corolarios.

Este tipo de presentación teórica imita la estructura de la geometría de Euclides, desarrollada en su obra «Elementos», la cual establece un sistema de demostración axiomático-deductivo que Spinoza retoma para fundamentar matemáticamente sus ideas metafísicas y éticas. A continuación, veremos un ejemplo del procedimiento geométrico aplicado por Spinoza en su «Ética»:

En la proposición XIV, de la primera parte «Sobre Dios», Spinoza establece:

• Proposición: «No puede darse ni concebirse sustancia alguna excepto Dios».
• Corolario 1: «De aquí se sigue muy claramente: primero, que Dios es único, esto es que, en la naturaleza, hay una sola sustancia y que esta es absolutamente infinita».
• Corolario 2: «Se sigue, segundo: que la cosa extensa y la cosa pensante, o bien son atributos de Dios, o bien afecciones de los atributos de Dios».

Citar este artículo

Aci, E. M. (26 de septiembre de 2024). Definición de corolario. Concepto y usos en matemática, lógica y filosofía. Definicion.com. https://definicion.com/corolario/